Power BI DAX 统计学

DAX多元线性回归与参数调优

by Davis ZHANG

04-06, 2019

阅读 ()

LEVEL: 困难

一、简述

本文主要介绍在利用PowerBI进行时间序列分析时，如何使用DAX完成多变量的线性回归预测。关于线性回归，通常分为简单线性回归与多元线性回归，前者只有一个自变量而后者大于一个自变量。对于PowerBI的简单线性回归，国外早已有人发表了相关介绍，但对于多元线性回归，我并没有在Google和百度上找到关于这方面的系统性介绍(注：不包括使用R&Python接口或可视化控件完成的方法)，因此我只能自己完成这一计算。下文将主要介绍使用DAX完成多元(二元为例)线性回归，并且将在此引入”Ridge回归”和”Lasso回归”中的模型调优思路。

二、多元线性回归公式推导

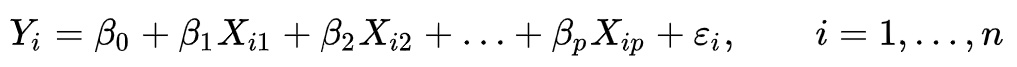
模型如下：在这里插入图片描述

DAX无法进行矩阵运算，因此回归公式参照克莱姆法则(不是史莱姆)。以二元回归为例，其目的是通过对现有数据集的计算，得出其中的β0，β1及β2的最优解，公式推导如下：

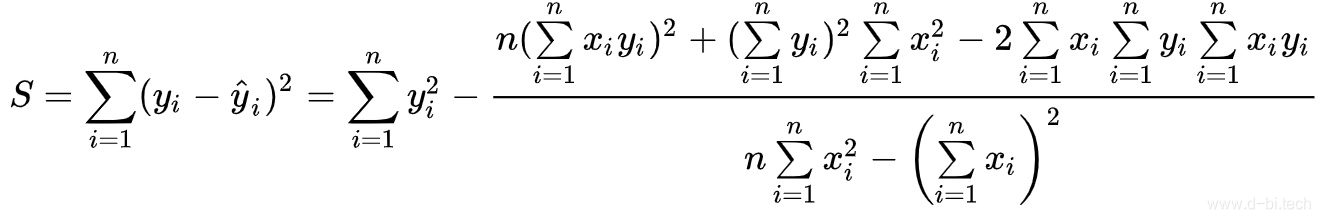
在这里插入图片描述

依据此公式，在DAX中进行运算，即可完成回归。

三、本文数据集简介

数据集下载自Tableau论坛,本案例使用的数据集为”Superstore.xls” 主表结构如下：

在这里插入图片描述

其中日期将做为首个自变量，销量将作为因变量(即预测目标)

在这里插入图片描述

四、执行二元回归

通过观察数据集，第二个自变量选择[月份]。依据前文的二元回归推导公式，完成代码如下：

Binary Linear Regression = 
VAR VT =
FILTER (
SELECTCOLUMNS(
SUMMARIZE(ALLSELECTED('Date'),'Date'[Date],'Date'[Month Number]),
"VT[X1]", 'Date'[Date],
"VT[X2]", 'Date'[Month Number],
"VT[Y]",'Orders'[Qty]
),
AND (
NOT ( ISBLANK ( VT[X1] ) ),
AND(
NOT ( ISBLANK ( VT[X2] ) ),
NOT ( ISBLANK ( VT[Y] ) )
))
)
VAR Average_X1 =
AVERAGEX ( VT, VT[X1] )
VAR Average_X2 =
AVERAGEX ( VT, VT[X2] )
VAR Average_Y =
AVERAGEX ( VT, VT[Y] )
VAR Sum_X1_2 =
SUMX ( VT, (VT[X1] - Average_X1) ^ 2 )
VAR Sum_X2_2 =
SUMX ( VT, (VT[X2] - Average_X2) ^ 2 )
VAR Sum_X1Y =
SUMX ( VT, (VT[X1] - Average_X1) * (VT[Y] - Average_Y))
VAR Sum_X2Y =
SUMX ( VT, (VT[X2] - Average_X2) * (VT[Y] - Average_Y))
VAR X12 = 
SUMX( VT, (VT[X1] - Average_X1)*(VT[X2] - Average_X2))
VAR Beta1 =
DIVIDE (
Sum_X1Y*Sum_X2_2 - sum_x2y*X12,
Sum_X1_2*Sum_X2_2 - X12 ^ 2
)
VAR Beta2 =
DIVIDE (
Sum_X2Y*Sum_X1_2 - sum_x1y*X12,
Sum_X1_2*Sum_X2_2 - X12 ^ 2
)
VAR Intercept =
Average_Y - Beta1 * Average_X1 - Beta2 * Average_X2
VAR Result = 
SUMX (
SUMMARIZE('Date','Date'[Date],'Date'[Month Number]),
Intercept + Beta1 * 'Date'[Date] + Beta2 * 'Date'[Month Number]
)
RETURN
Result

结果如下图红线所示：

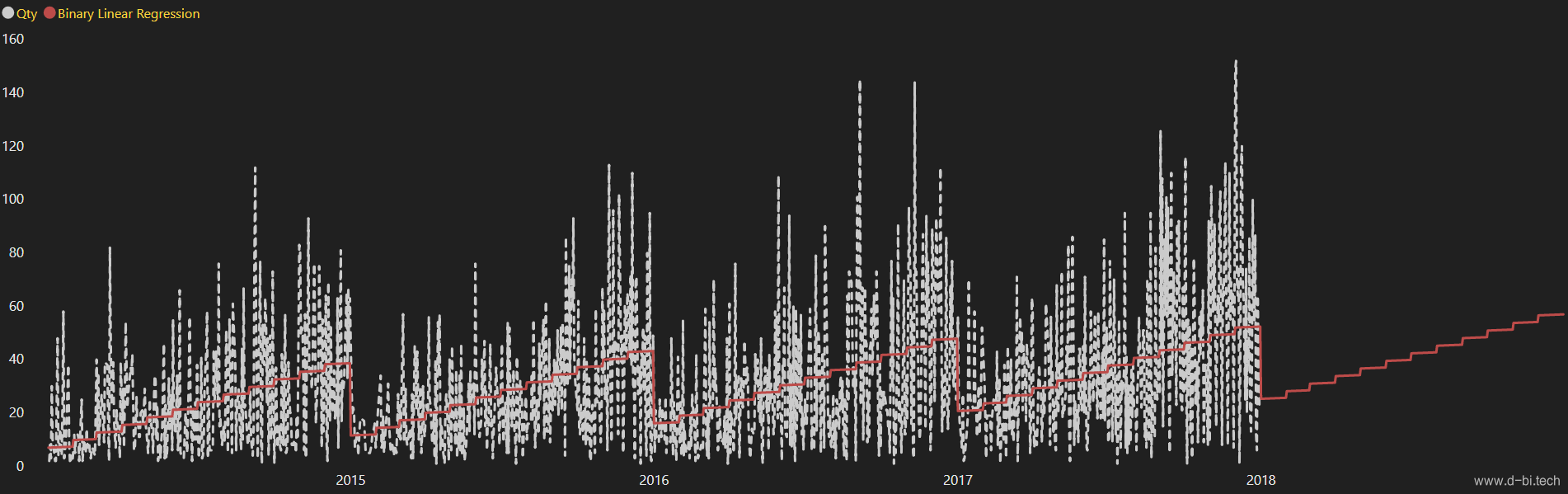
在这里插入图片描述

五、评估回归模型

模型建立完成后，我们需要评估它的拟合效果。我在此引入两个指标： 1.RMSE(均方根误差) – 越小越好 2.R^2(拟合优度) – 通常越接近1越好其中，RMSE(=RMSD)公式如下，即数据集中每条记录的拟合值与实际值的均方根误差：

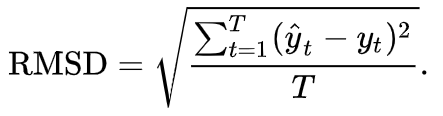
在这里插入图片描述

R^2即相关系数的平方:

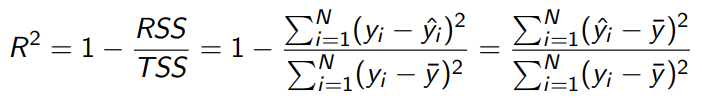
在这里插入图片描述

TSS:总离差平方和 ESS:回归平方和 RSS:残差平方和

依据上述公式，分别完成RMSE和R^2的代码：

RMSE = 
VAR VT =
SUMMARIZE(
ALLSELECTED('Date'),'Date'[Date],'Date'[Month Number])
RETURN
SQRT(
    divide(
        SUMX(VT,
            ('Orders'[Binary Linear Regression] - 'Orders'[Qty]) ^ 2),
        COUNTROWS(VT)))

R^2 = 
VAR VT =
SUMMARIZE(ALLSELECTED('Date'),'Date'[Date],'Date'[Month Number])
VAR
ESS = SUMX(VT,POWER('Orders'[Binary Linear Regression]-AVERAGEX(VT,[Qty]),2))
VAR
TSS = SUMX(VT,POWER([Qty]-AVERAGEX(VT,[Qty]),2))
RETURN
DIVIDE(ESS,TSS)

执行效果如下，可知该模型的拟合效果并不乐观：

在这里插入图片描述

六、模型调优

针对于线性回归的优化，有两种主流方法：1.Lasso回归 2.岭回归(Ridge回归) 这两种方法分别为模型加上了L1正则项和L2正则项。本文不讨论复杂的统计学，只在乎如何高效地使用DAX解决这个模型调优的问题。实际上，这两种方法都是通过添加惩罚项来压低模型的某些系数，前者则可以直接把不重要的系数压缩至0，因此，此算法本质上就是对模型中的各β系数选择性的压缩。另外，DAX本身并不是用于算法的语言，结合考虑到代码最后运行的性能，我们可以直接在模型各β系数上面乘以一个变量来达到效果，而无需执行复杂的推导计算。在PowerBI中创建参数来作为这个变量的值，这样我们就可以在可视化界面去调整变量的值，进而达到对模型手动调优的效果。因此，在前文二元回归模型的代码基础上修改后如下：

Manual Binary Regression = 
VAR R = '_Slope'[Regular factor Value] --调节斜率
VAR A = 'α'[α Value] --调节第一个参数
VAR B = 'β'[β Value] --调节第二个参数
VAR VT =
FILTER (
SELECTCOLUMNS(
SUMMARIZE(ALLSELECTED('Date'),'Date'[Date],'Date'[Month Number]),
"VT[X1]", 'Date'[Date],
"VT[X2]", 'Date'[Month Number],
"VT[Y]",'Orders'[Qty]
),
AND (
NOT ( ISBLANK ( VT[X1] ) ),
AND(
NOT ( ISBLANK ( VT[X2] ) ),
NOT ( ISBLANK ( VT[Y] ) )
))
)
VAR Average_X1 =
AVERAGEX ( VT, VT[X1] )
VAR Average_X2 =
AVERAGEX ( VT, VT[X2] )
VAR Average_Y =
AVERAGEX ( VT, VT[Y] )
VAR Sum_X1_2 =
SUMX ( VT, (VT[X1] - Average_X1) ^ 2 )
VAR Sum_X2_2 =
SUMX ( VT, (VT[X2] - Average_X2) ^ 2 )
VAR Sum_X1Y =
SUMX ( VT, (VT[X1] - Average_X1) * (VT[Y] - Average_Y))
VAR Sum_X2Y =
SUMX ( VT, (VT[X2] - Average_X2) * (VT[Y] - Average_Y))
VAR X12 = 
SUMX( VT, (VT[X1] - Average_X1)*(VT[X2] - Average_X2))
VAR Beta1 =
DIVIDE (
Sum_X1Y*Sum_X2_2 - sum_x2y*X12,
Sum_X1_2*Sum_X2_2 - X12 ^ 2
) * A -- 乘以参数A
VAR Beta2 =
DIVIDE (
Sum_X2Y*Sum_X1_2 - sum_x1y*X12,
Sum_X1_2*Sum_X2_2 - X12 ^ 2
) * B -- 乘以参数B
VAR Intercept =
Average_Y - Beta1 * Average_X1 - Beta2 * Average_X2
VAR Result = 
SUMX (
SUMMARIZE('Date','Date'[Date],'Date'[Month Number]),
Intercept + Beta1 * 'Date'[Date] + Beta2 * 'Date'[Month Number]
)
RETURN
Result * (1-1/R) --乘以斜率参数

执行效果如下(注：调整后的模型如深蓝色曲线所示，RMSE和R^2也改为针对该模型的评估值)：

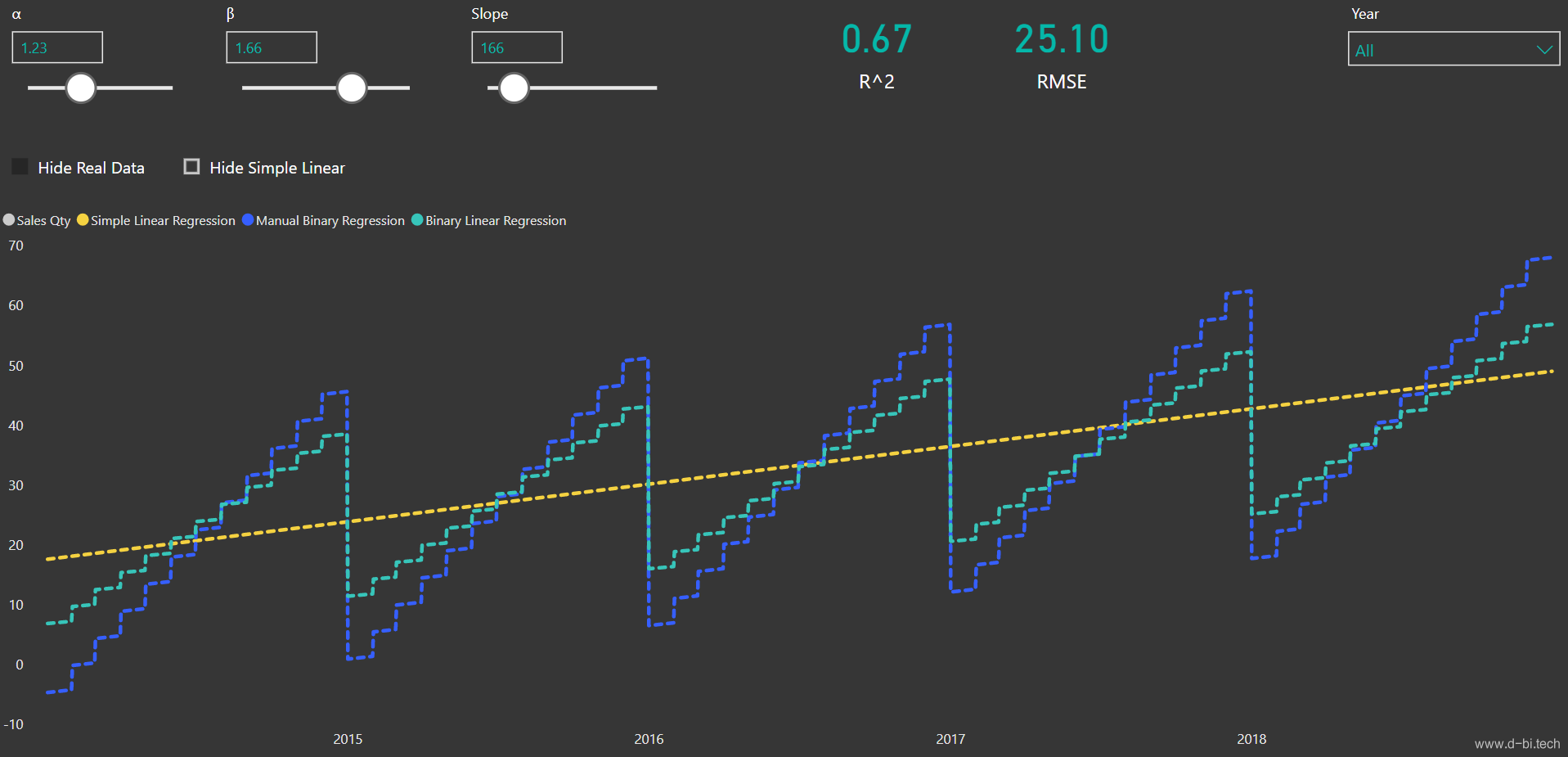
在这里插入图片描述

至此，我们完成了对该二元线性回归模型的手动调优，我们可以调节其中的参数，然后观察评估结果。本文到此本该结束，但是后来我觉得这样调整有点盲目，调整参数应该有一个直观科学的参考，这样才能提高使用效率。因此我做了一个模型优化参考图，本文以第一个参数(即日期)为例，以该参数作为自变量(X轴)，R^2和RMSE作为因变量(Y轴)，用以直观地对模型调优提供参考：

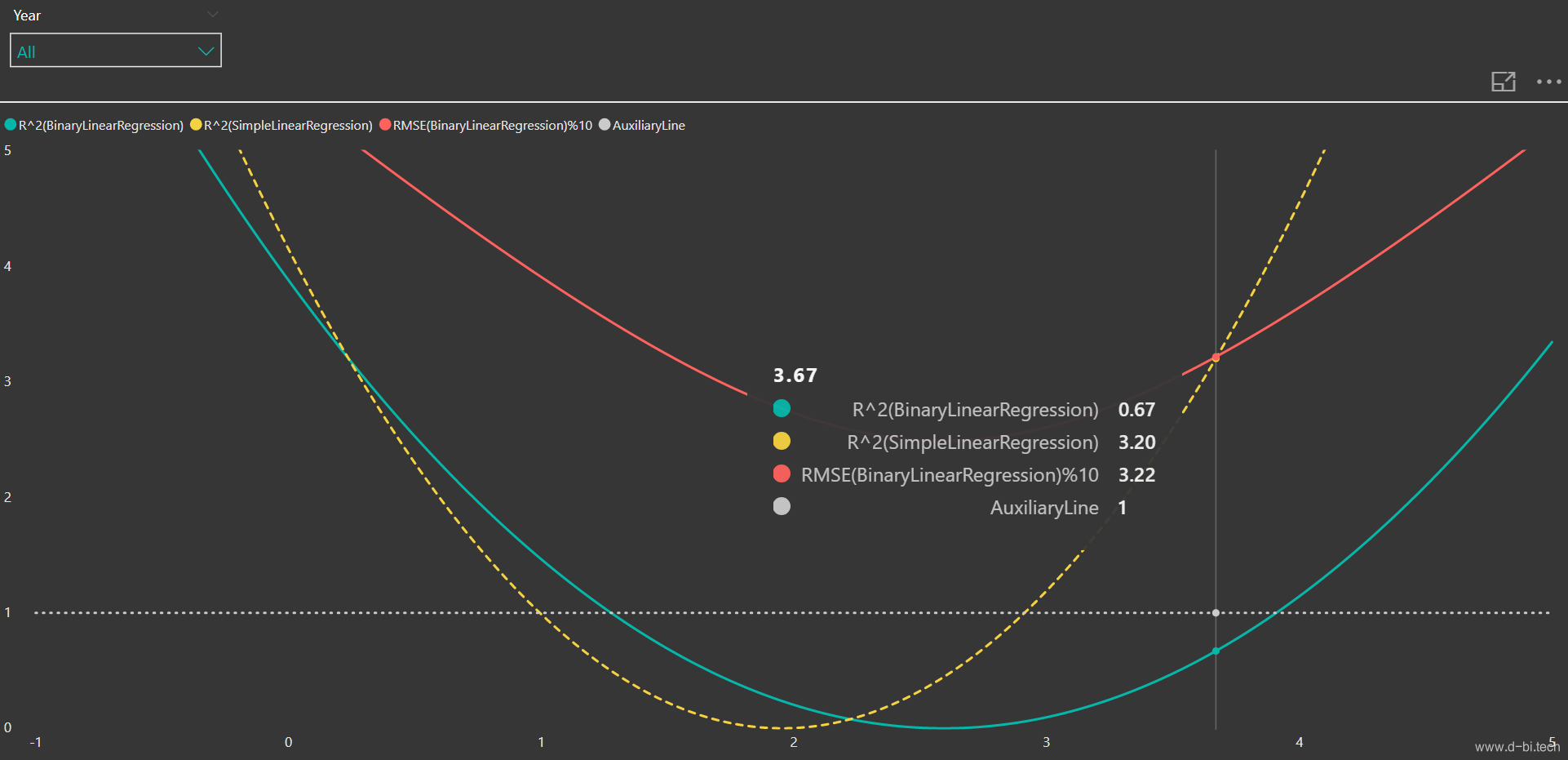
在这里插入图片描述

*注：由于RMSE远大于R^2,为使RMSE和R^2更易于观察，图中的RMSE值压缩至原来的十分之一。当然你也可以考虑使用双轴图，但目前来讲PowerBI自带的双轴图控件并没有Tooltips

七、总结

注：此段相对原文有修改

至此，我们已经知道了如何用DAX进行多元线性回归以及进行模型调优的方法。在此我只是介绍了我自己的方法，要发挥出DAX的强大潜力，大家尚需努力探索。但如果是真的要应用一些机器学习算法，我并不推荐DAX，我知道它可以实现，就像本文展示的那样，但它太过消耗计算机内存，如果数据量太大则性能实在堪忧。因此，如果你是一名DAX爱好者或为了学习线性回归算法本文是很好的资料，但如果是实际应用，我认为使用R或Python等语言先把结果集算出来是更好的方式。我在后来还做了三元线性回归，文章到此处篇幅已经较长，这部分公式在此省略了，如果感兴趣可以点击右下角到我的LinkedIn页面查找，如果喜欢欢迎顺手点个赞:D

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可
关于本文，如有问题或建议，欢迎您前往知乎微软BI圈发帖（备注本文链接），我将尽快回复

DAX多元线性回归与参数调优

一、简述

二、多元线性回归公式推导

三、本文数据集简介

四、执行二元回归

五、评估回归模型

六、模型调优

七、总结

用DAX构建筛选信息栏

Power BI之SVG自定义可视化